Contents
- 1 Задание 1. Вариант 252 Ларина ЕГЭ 2019 по математике
- 2 Задание 2
- 3 Задание 3
- 4 Задание 4. Вариант 252 Ларина ЕГЭ 2019 по математике
- 5 Задание 5
- 6 Задание 6
- 7 Задание 7
- 8 Задание 8
- 9 Задание 9
- 10 Задание 10. Вариант 252 Ларина ЕГЭ 2019 по математике
- 11 Задание 11
- 12 Задание 12. Вариант 252 Ларина ЕГЭ 2019 по математике
- 13 Задание 13
- 14 Задание 14
- 15 Задание 15. Вариант 252 Ларина ЕГЭ 2019 по математике
- 16 Задание 16. Вариант 252 Ларина ЕГЭ 2019 по математике
- 17 Задание 17. Вариант 252 Ларина ЕГЭ 2019 по математике
- 18 Задание 18. Вариант 252 Ларина ЕГЭ 2019 по математике
- 19 Задание 19. Вариант 252 Ларина ЕГЭ 2019 по математике
- 20 Видео: Разбор Варианта ЕГЭ Ларина №252 (№1-15)
- 21 Видео: Разбор Варианта ЕГЭ Ларина №252 (№16-19)
Задание 1. Вариант 252 Ларина ЕГЭ 2019 по математике
Двое решают, как им обойдет дешевле доехать из Москвы до Санкт‐Петербурга – на поезде или на автомобиле. Билет на поезд стоит 1500 рублей на одного человека. Автомобиль расходует 6 литров на 100 км пути, расстояние по шоссе равно 700 км, а цена бензина равна 43 рубля за литр. Сколько рублей придется заплатить за самую дешевую поездку за двоих?
Решение
2 билета: 3000 — стоимость поездки на автобусе на 2-их.
6∗7∗43 = 1806 — стоимость поездки на автомобиле.
Ответ: 1806.
Задание 2
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в период с мая по декабрь 1973 года включительно. Ответ дайте в градусах Цельсия.
Решение

Границы где смотрим температуру отмечены красным (так как май-5-ый месяц по счету). В итоге, наименьшая температура равна -6 градусов Цельсия.
Ответ: -6.
Задание 3
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см X 1 см (см. рис.).
Ответ дайте в квадратных сантиметрах.
Решение

Ответ: 6.
Задание 4. Вариант 252 Ларина ЕГЭ 2019 по математике
В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятность двух осечек. Результат округлите до сотых.
Решение
Вероятность первой осечки равна 2/6 а вероятность второй (при условии что была первая) равна 1/5.
Тогда искомая вероятность равна P = 2/6∗1/5=0.07.
Ответ: 0,07.
Задание 5
Решите уравнение:

Если корней несколько, то в ответе укажите меньший корень.
Решение

x1 = 10, x2 = -3.
Ответ: 10.
Задание 6
В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей напротив основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.
Решение
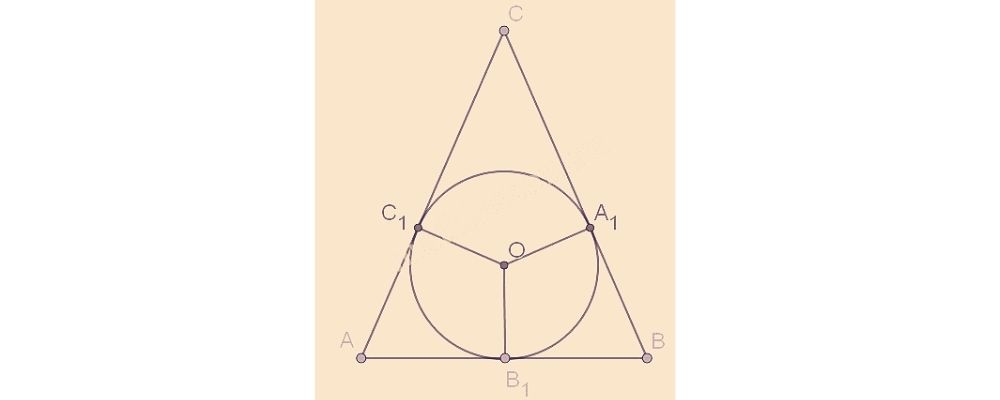

Ответ: 30.
Задание 7
Функция f(x) определена на всей числовой прямой и является периодической с периодом 4.

На рисунке изображен график этой функции при -1 ≤ x ≤ 3. Найдите значение выражения: f(-3)*f(1)*f(11).
Решение
С учетом периодичности функции:
;
;
Тогда:
Ответ: 4.
Задание 8
Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Решение


Ответ: 1,5.
Задание 9
Вычислите:
Решение

Ответ: 0,2.
Задание 10. Вариант 252 Ларина ЕГЭ 2019 по математике
Катер должен пересечь реку шириной L=100м и со скоростью течения u= 5,0 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением t=(L/u)*ctga, где a — острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом a (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
Решение
Ответ: 45.
Задание 11
Секретарю фирмы поручили разослать письма адресатам по списку. Секретарь, отдав своему помощнику часть списка, содержащую 80% адресатов, взял оставшуюся часть себе и разослал письма по своей части списка за время, в 6 раз меньшее, чем помощник – по своей.
Сколько процентов списка адресатов секретарь должен был сразу отдать помощнику (взяв себе остальные), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое время?
Решение
Пусть S-кол-во адресатов, x-число адресатов в час секретарем , y-помощником.

Следовательно скорость секретаря в полтора раза выше объем должна взять в полтора раза больше.
Пусть V — объем работы помощника:
%
% помощнику отдать.
Ответ: 40.
Задание 12. Вариант 252 Ларина ЕГЭ 2019 по математике
Найдите наибольшее значение функции:

на промежутке [1;7]
Решение

Ответ: 1.
Задание 13
- а) Решите уравнение:

- б) Укажите корни этого уравнения, принадлежащие отрезку: [-7π;11π/2].
Решение

Ответ:
Задание 14
Точки M,N и P лежат на боковых ребрах правильной треугольной призмы ABCA1B1C1 и делят их в отношении:
, ,
- А) В каком отношении делит объем призмы плоскость, проходящая через точки M,N и P ?
- Б) Докажите, что MNP ‐ прямоугольный треугольник, если сторона основания призмы равна 2\sqrt{10} , а боковое ребро равно 60.
Решение
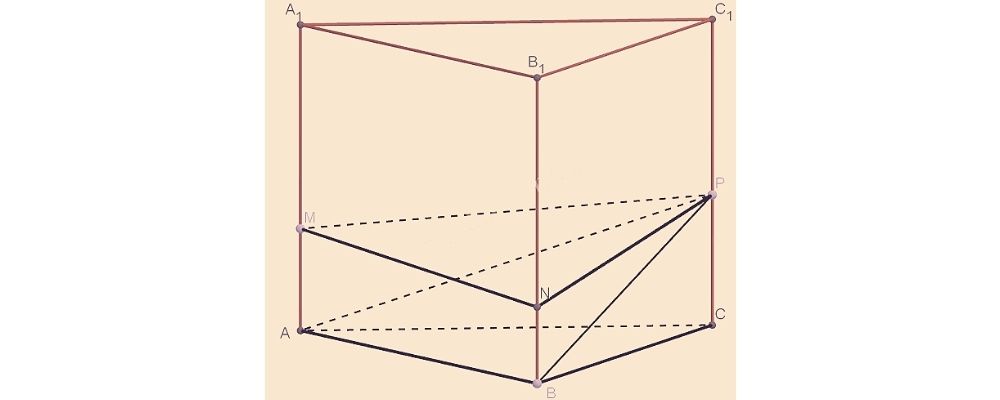



Ответ: 59/129.
Решите неравенство:

Решение

Ответ:
Задание 16. Вариант 252 Ларина ЕГЭ 2019 по математике
Точка N делит диагональ трапеции ABCD в отношении CN:NA=2:1. Длины оснований ВС и AD относятся как 1:3. Через точку N и вершину D проведена прямая, пересекающая боковую сторону АВ в точке М.
- А) Какую часть площади трапеции составляет площадь четырехугольника MBCN?
- Б) Найдите длину отрезка MN, если MD=9.
Решение



Ответ: А) 7/32; Б) 1.
Задание 17. Вариант 252 Ларина ЕГЭ 2019 по математике
В офисном здании 8 этажей, на каждом из которых, кроме первого, находится кабинет начальника отдела. Управляющая жилищная компания объявила что в день профилактического ремонта лифта он сделает всего один подъем сразу всех начальников на один, указанный ими этаж. После подъема начальники будут вынуждены идти в свои кабинеты по лестнице.
В качестве компенсации за причиненные неудобства за каждый необходимый подъем на очередной этаж по лестнице каждому начальнику будет начислено 200 рублей. За каждый аналогичный спуск – 100 рублей. Этаж необходимо выбрать тк, чтобы общая сумма компенсаций была минимальной. Укажите в рублях эту сумму.
Решение
Пусть лифт остановится на n-ом этаже. Тогда сверху будет (8-n) этажей, а снизу будет (n-2) этажей. Общая сумма компенсации будет равна:
S(n) = 200(1+2+…+(8−n))+100(1+2+…(n−2)).
Видим арифметические прогрессии:
200(1+2+…+(8−n)) = (200∗(1+8−n)/2)∗(8−n) = 100∗(9−n)∗(8−n).
100(1+2+…(n−2)) = (100∗ (1+n−2)/2)∗(n−2) = 50∗(n−1)(n−2).
S(n ) = 50(3n²−37n+146) — это парабола, ветви вверх, Стандартная 12 задача на нахождение точки минимума. 2 <= n <= 8
(n0=37/6 — точка минимума, так как n-целое, то n = 6 или 7, проверяем, n = 6)
Ответ: 6 этаж, 1600 рублей.
Задание 18. Вариант 252 Ларина ЕГЭ 2019 по математике
Найдите все значения параметра p , при которых уpавнение:

имеет хотя бы один корень.
Решение

С учетом , что имеем следующие возможные расположения графика, при котором будет хотя бы одно решение из (1):




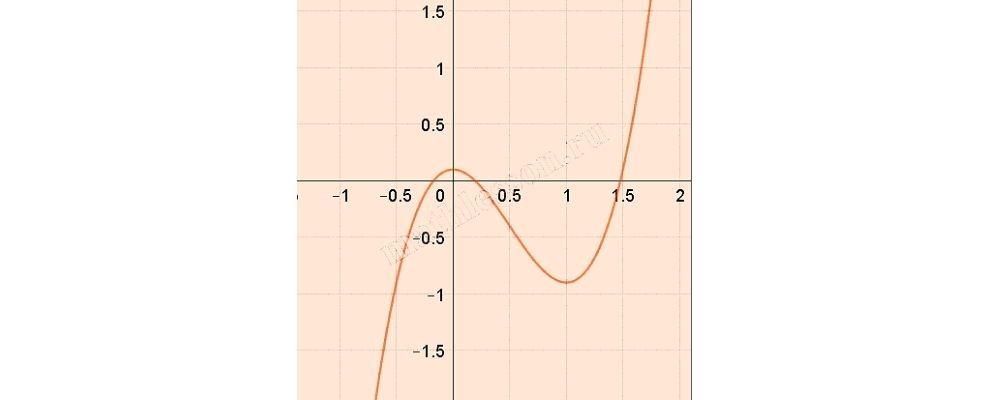


Тогда . При этом . С учетом, что на промежутке от [-1;0) — убывает, а на (0;1] — возрастает, то
Ответ: (0;5]
Задание 19. Вариант 252 Ларина ЕГЭ 2019 по математике
На доске написаны числа 3 и 5. За один ход разрешено заменить написанную на доске пару чисел a и b парой чисел 2a-1 и a+b+1 (например, из пары чисел 3 и 5 за один ход можно получить либо числа 5 и 9, либо числа 9 и 9).
- А) Может ли получиться так, что после нескольких ходов на доске будут написаны числа 73 и 75?
- Б) Может ли получиться так, что после нескольких ходов одно из написанных на доске чисел будет равно 35?
- В) После 2017 ходов на доске получили пару чисел, не равных друг другу.
Какое наименьшее значение может иметь разность между большим и меньшим из этих чисел?
Решение
- а) Да, например:
(3; 5) → (9; 9) → (17; 19) → (37; 37) → (73; 75).
- б) Нет.
2a — 1 ≥ a и a + b + 1 > b поэтому как только оба числа в паре станут больше 35, дальше можно не перебирать.
На первом шаге можно получить:
(5; 9) или (9; 9).
На втором:
(9; 15), (17; 15) или (17; 19).
На третьем:
(17; 15), (29; 25), (33; 33), (29; 33), (33; 37), (37; 37).
Все пары, кроме первой, дадут числа, большие 35. Первая может дать (33; 43) и после еще одного хода числа превысят 35.
- в) Если числа дают остатки 1 и 3 от деления на 4, то их сумма кратна 4, поэтому 2a — 1, 2b — 1, a + b +1 дают остаток 1 при делении на 4.
Если же оба числа дают остаток 1 при делении на 4, то 2a — 1 или 2b — 1 дает остаток 1, а a + b +1 дает остаток 3 при делении на 4.
Итак, пары остатков чередуются — после нечетного хода это (1; 1) после четного — (1; 3). Поскольку числа не равны и дают одинаковый остаток от деления на 4, разность между ними не меньше 4. Этого достичь можно. Первым ходом получим пару (5; 9). А затем с парой (x; x + 4) будет проделывать пары ходов:
(x; x + 4) → (2x — 1; 2x + 5) → (4x + 5; 4x + 9).
после которых разность чисел в паре будет сохраняться.
Ответ: а) да; б) нет; в) 4.
Видео: Разбор Варианта ЕГЭ Ларина №252 (№1-15)
Видео: Разбор Варианта ЕГЭ Ларина №252 (№16-19)

