Задание 1
Больному прописано лекарство, которое нужно пить по 0,5 г 2 раза в день в течение 19 дней. Лекарство выпускается в упаковках по 10 таблеток по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
Решение
В день 0,5 * 2 = 1 грамм.
За 19 дней 1 * 19 = 19 грамм. В пачке 10*0,5=5 грамм.
Кол-во упаковок : 19/5 пачки лекарства.
Ответ: 4.
Задание 2
На рисунке жирными точками показана цена цинка на момент закрытия биржевых торгов во все рабочие дни с 5 по 18 февраля 2008 года. По горизонтали указываются числа месяца, по вертикали – цена тонны цинка в долларах США.
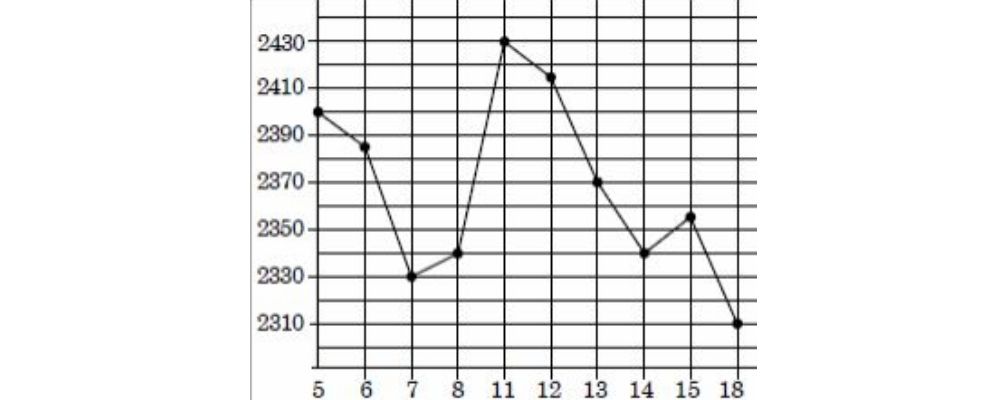
Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену цинка на момент закрытия торгов в период с 6 по 15 февраля (в долларах США за тонну).
Решение

7- го числа по 2330 долларов.
Ответ: 2330.
Задание 3
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см * 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.

Решение
Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне. Поэтому:
S = ½* 3* 8 = 12 см2.
Ответ: 12.
Задание 4
Решение
Вероятность быть исправленной:
1 — 0,04 = 0,96.
Вероятность быть при этом быть заблокированной:
0,96*0,01 = 0,0096.
Вероятность заблокировать неисправную:
0,04*0,95 = 0,038.
Общая вероятность:
0,038 + 0,0096 = 0,0476.
Ответ: 0,0476.
Задание 5
Решите уравнение √(
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Решение

Ответ: 1.
Задание 6
Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение

Ответ: 39.
Задание 7
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0 .

Решение
Значение производной есть тангенс угла между касательной, проведенной в заданную точку и осью Ох.
Достроим: = 2.

Так как функция убывает, то значение производной будет отрицательное -2.
Ответ: -2.
Задание 8
Площадь боковой поверхности конуса равна 16 см2. Радиус основания конуса уменьшили в 4 раза, а образующую увеличили в 2 раза. Найдите площадь боковой поверхности получившегося конуса. Ответ дайте в см2
Решение

Ответ: 8.
Задание 9
Найдите значение выражения:
log411*log1116.
Решение

Ответ: 2.
Задание 10
Небольшой мячик бросают под острым углом a к плоской горизонтальной поверхности земли. Максимальная высота полета мячика, выраженная в метрах, определяется формулой:

где v0=26м/c — начальная скорость мячика, а g -ускорение свободного падения (считайте g=10 ).
При каком наименьшем значении угла a (в градусах) мячик пролетит над стеной высотой 15,9 м на расстоянии 1 м?
Решение

Ответ: 45.
Задание 11
Брюки дороже рубашки на 30% и дешевле пиджака на 22%. На сколько процентов рубашка дешевле пиджака?
Решение

Ответ: 40.
Задание 12
Найдите наименьшее значение функции:

на отрезке [137;156]
Решение

Ответ: -565.
Задание 13
а) Решите уравнение:

б) Укажите корни этого уравнения, принадлежащие отрезку:
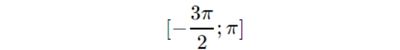
Решение
а) Найдем ограничения по х:

б)Отметим полученные корни в общем виде на окружности, а так же интервал, данный по условию (он включает в себя полностью всю окружность (синий цвет) и сектор во второй четверти (красный цвет))

Найдем корни, которые попадут в данный промежуток:

Ответ:
Задание 14
В правильной треугольной призме ABCA1B1C1 сторона основания AB=6√3 . На ребре BC отмечена точка М так, что BC:MC=3:1 , а на ребре AC отмечена точка N так, что AN:NC=2:1 .
Точка К середина ребра АВ.
а) Доказать что ОК параллельна плоскости MNC1 , где О-центр вписанной окружности треугольника A1B1C1 .
б)Найти угол между прямой ОК и плоскостью основания, если площадь треугольника MNC1 равна 6√3
Решение


Ответ: 60.
Задание 15
Решите неравенство:

Решение

Рассмотрим промежутки по отдельности и воспользуемся свойствами логарифмических функций:

Аналогично , но при всех х из полученных промежутков, следовательно, неравенство выполняется в обоих случаях и .
Ответ:
Задание 16
В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K . Точки L и M являются соответственно серединами сторон BC и AD . Отрезок LM содержит точку K . Четырехугольник ABCD таков, что в него можно вписать окружность.
а) Докажите, что четырехугольник ABCD трапеция.
б) Найдите радиус этой окружности, если AB=3 , AC=√13 и LK:KM=1:3
Решение




Ответ: 1,5.
Задание 17
Алексей решил взять кредит в банке 100 тысяч рублей на 4 месяца под 5% в месяц. Существуют две схемы выплаты кредита. По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 5%), затем Алексей переводит в банк фиксированную сумму и в результате выплачивает весь долг четырьмя равными платежами.
По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 5%, а затем уменьшается на сумму, уплаченную Алексеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.
Какую схему выгоднее выбрать Алексею?
Сколько рублей будет составлять эта выгода?
Решение
Для равных платежей:
Все преобразования с суммами долга занесём в таблицу:
| n | Долг после начисления процентов | Сумма долга после очередной выплаты |
| 1 | Sk | |
| 2 | ||
| 3 | ||
| 4 |
По условию задачи через 4 месяца долг выплачен полностью, то есть:

Для равномерного погашения долга:
По условию задачи каждый месяц долг уменьшается на одну и ту же сумму, равную 1000000:4 = 25000 (тыс. рублей),
тогда оставшиеся суммы долга равны:
- 1000000;
- 75000;
- 50000;
- 25000.
на начало каждого месяца кредитования соответственно.
Каждый месяц Алексей выплачивает четверть суммы, взятой в кредит (фиксированная часть выплаты) + проценты, начисленные на оставшуюся на этот месяц сумму долга.
Вся выплаченная банку сумма в этом случае составит: S2 = 100000 + 0,05 ∙ (100000 + 75000 + 50000 + 25000) = 100000 + 0,05 ∙ 250000 = 100000 + 12500 = 112500 (руб. )
Так как 112805 > 112500, то выгоднее вторая схема, на 112805 — 112500 = 305 рублей (приближенное значение с учетом расчетов)
Ответ: 2 схема; 305.
Задание 18
Найдите все значения параметра a , при каждом из которых уравнение:

имеет хотя бы один корень.
Решение

Рассмотрим функцию f(y): так как там есть модуль и параметр, то будет несколько вариантов раскрытия:

Изображение графика:

Схематичное изображение графика:
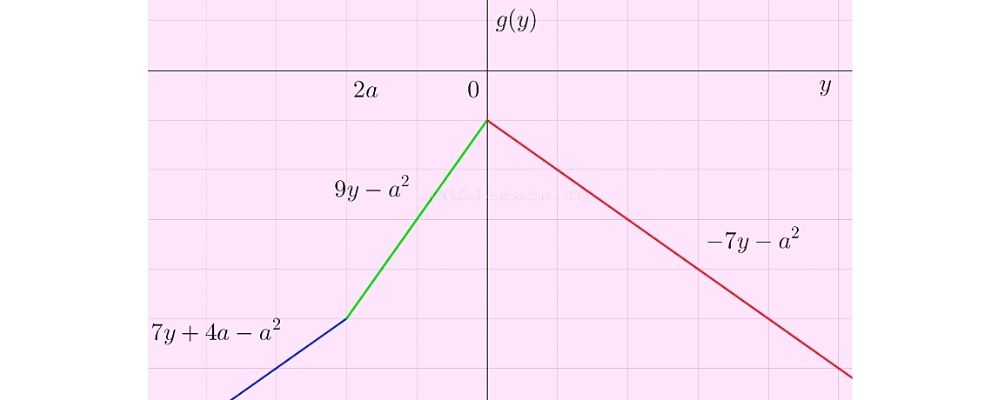
И тут максимальное значение в координате : fmax=f(0).
То есть, независимо от значения a максимальное значение при .
Тогда , чтобы были решения (графическая интерпретация):

Тогда:

Ответ: 2.



