Contents
- 1 Задание №1
- 2 Задание №2. Решение варианта №196 ОГЭ по математике Ларин
- 3 Задание №3. Решение варианта №196 ОГЭ по математике Ларин
- 4 Задание №4. Решение варианта №196 ОГЭ по математике Ларин
- 5 Задание №5
- 6 Задание №6. Решение варианта №196 ОГЭ по математике Ларин
- 7 Задание №7
- 8 Задание №8. Решение варианта №196 ОГЭ по математике Ларин
- 9 Задание №9. Решение варианта №196 ОГЭ по математике Ларин
- 10 Задание №10. Решение варианта №196 ОГЭ по математике Ларин
- 11 Задание №11. Решение варианта №196 ОГЭ по математике Ларин
- 12 Задание №12. Решение варианта №196 ОГЭ по математике Ларин
- 13 Задание №13. Решение варианта №196 ОГЭ по математике Ларин
- 14 Задание №14. Решение варианта №196 ОГЭ по математике Ларин
- 15 Задание №15
- 16 Задание №16
- 17 Задание №17
- 18 Задание №18
- 19 Задание №19
- 20 Задание №20. Решение варианта №196 ОГЭ по математике Ларин
- 21 Задание №21
- 22 Задание №22
- 23 Задание №23
- 24 Задание №24
- 25 Задание №25
- 26 Задание №26
- 27 Видео: Разбор Варианта ОГЭ Ларина №196 (№1-20)
- 28 Видео: Разбор Варианта ОГЭ Ларина №196 (№21-26)
Задание №1
Найдите значение выражения:

Решение

Ответ: 150.
Задание №2. Решение варианта №196 ОГЭ по математике Ларин
| Отправление от ст. Нара | Прибытие на Киевский вокзал |
| 06:35 | 07:59 |
| 07:05 | 08:15 |
| 07:28 | 08:30 |
| 07:34 | 08:57 |
Студент Васильев выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве. Путь от вокзала до университета занимает 40 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студенту:
- 06:35.
- 07:05.
- 07:28.
- 07:34.
Решение
Путь от вокзала до университета занимает 40 минут, поезд должен прибыть на вокзал не позднее 08:20. Этому условию удовлетворяют поезда, отправляющиеся от станции Нара в 6:35 и 7:05. Время отправления самого позднего из подходящих поездов 7:05.
Правильный ответ под номером 2.
Ответ: 2.
Задание №3. Решение варианта №196 ОГЭ по математике Ларин
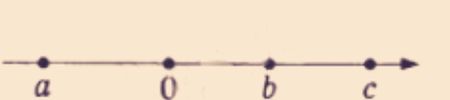
На координатной прямой отмечены числа a , b и c. Какое из следующих утверждений об этих числах верно?
Варианты ответа:
Решение

Ответ: 3.
Задание №4. Решение варианта №196 ОГЭ по математике Ларин
Расположите в порядке убывания числа: 9,5; 3√10; √95;
Варианты ответа:
Решение
⇒ порядке убывания:
2 вариант ответа.
Ответ: 2.
Задание №5
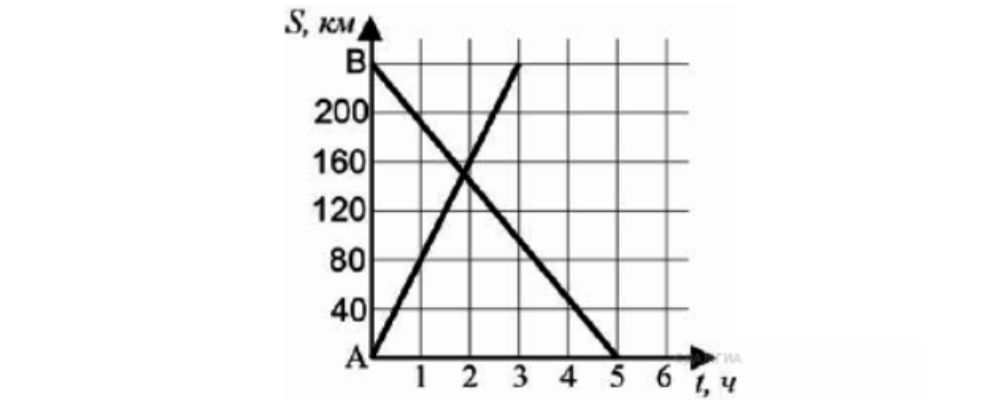
На рисунке изображен график движения автомобиля из пункта А в пункт B и автобуса из пункта B в пункт A. На сколько километров в час скорость автомобиля больше скорости автобуса?
Решение
240/3 = 80 км/ч скорость авто.
240/5 = 48 км/ч скорость автобуса.
80 — 48 = 32 48 км/ч.
Ответ: 32.
Задание №6. Решение варианта №196 ОГЭ по математике Ларин
При каком значении x значения выражений 28-8x и -3x+20 равны?
Решение
Ответ: 1,6.
Задание №7
Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 80 млн. рублей. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Решение
Частным акционерам принадлежит 100 — 60 = 40% акций ⇒
сумма в рублях составит:

Ответ: 32 млн рублей.
Задание №8. Решение варианта №196 ОГЭ по математике Ларин

На диаграмме показан возрастной состав населения России. Определите по диаграмме, население какого возраста преобладает.
- 0-14 лет;
- 15-50 лет;
- 51-64 лет;
- 65 лет и более.
Решение
Более 40% — это почти более половины населения. Из рисунка видно, что этому соответствует самый большой сегмент с возрастом от 15 до 50 лет.
Ответ: 2.
Задание №9. Решение варианта №196 ОГЭ по математике Ларин
Антон бросает одновременно две игральные кости. Найдите вероятность того, что сумма выпавших очков кратна трём.
Решение
Всего: 6*6 = 36 исходов.
Благоприятные:
9 исходов (1+2; 1+5; 2+1; 2+4; 3+3; 3+6; 4+2; 5+1; 6+6).
Вероятность:
9/36=1/4=0,25.
Ответ: 0,25.
Задание №10. Решение варианта №196 ОГЭ по математике Ларин
На рисунке изображены графики функций вида y = ax²+c Установите соответствие между графиками функций и знаками коэффициентов a и c:
Решение
–ветви параболы вверх, — вниз.
— ордината точки пересечения графика функции и оси Oy больше 0, — меньше 0 ⇒
Ответ: 321.
Задание №11. Решение варианта №196 ОГЭ по математике Ларин
Арифметическая прогрессия задана условием:
.
Найдите a10
Решение
-0,9 +8 = 7,1.
Ответ: 7,1.
Задание №12. Решение варианта №196 ОГЭ по математике Ларин
Найдите значение выражения:

если ,
Решение

Ответ: 8.
Задание №13. Решение варианта №196 ОГЭ по математике Ларин
Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s=nl, где n — число шагов, l — длина шага. Какое расстояние прошел человек, если l=65 см, n=1800? Ответ выразите в километрах.
Решение
65 см = 0,65/1000 км.
км.
Ответ: 1,71.
Задание №14. Решение варианта №196 ОГЭ по математике Ларин
При каких значениях x значение выражения 6x-2 меньше значения выражения 7x+8?
Варианты ответа:
- x > − 10.
- x < − 10.
- x < − 6.
- x > − 6.
Решение
, ⇒ 1 вариант.
Ответ: 1.
Задание №15
В 48 м одна от другой растут две сосны. Высота одной 38 м, а другой — 18 м. Найдите расстояние (в метрах) между их верхушками.

Решение
м.
м.
:
Ответ: 52.
Задание №16
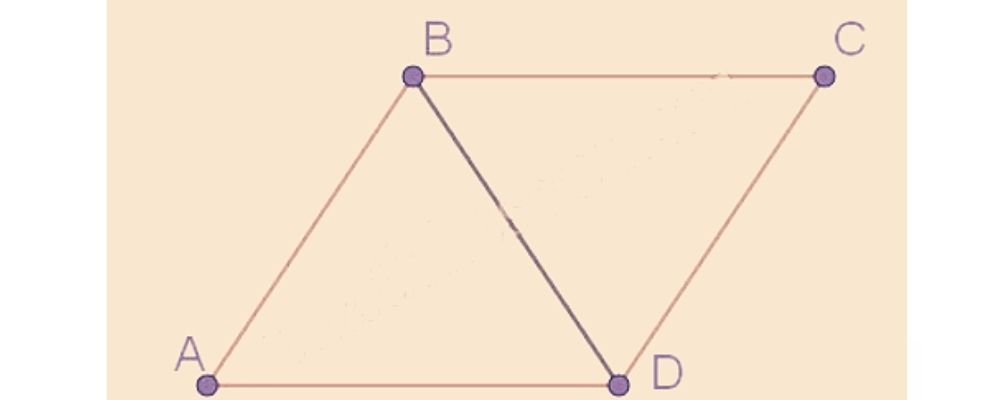
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 35º и 60º. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Решение
.
Ответ: 85º.
Задание №17

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что уголNBA = 48º. Найдите угол NMB. Ответ дайте в градусах.
Решение
∠NBA = 48° вписанный ⇒ дуга AN = 2 * 48° = 96°.
дуга NB = 180° — дуга AN = 180° — 96° = 84°.
∠NMB = 1/2 дуги NB = 84 /2 = 42.
Ответ: 42.
Задание №18

В прямоугольнике одна сторона равна 12, а диагональ равна 37. Найдите площадь прямоугольника.
Решение
: .
Ответ: 420.
Задание №19
В остроугольном треугольнике ABC высота AH равна 19√21 а сторона AB равна 95. Найдите cosB.
Решение

Ответ: 0,4.
Задание №20. Решение варианта №196 ОГЭ по математике Ларин
Какие из следующих утверждений верны?
- Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла;
- Если в треугольнике есть один острый угол, то этот треугольник остроугольный;
- Диагонали ромба равны.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Решение
- Верно.
- Неверно.
- Неверно.
Ответ: 1 утверждение верно.
Задание №21
Решите систему уравнений:
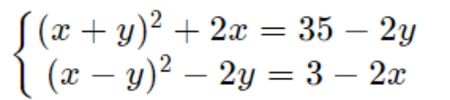
Решение

Получаем четыре пары решений: (-7;-3); (-7;1); ( 5;-3); (5;1).

Ответ: (-5;-2); (-3;-4); (1;4); (3;2).
Задание №22
Два велосипедиста выезжают одновременно навстречу друг другу из пунктов А и В, расстояние между которыми 27 км. Через час велосипедисты встречаются и, не останавливаясь, продолжают ехать с той же скоростью. Первый прибывает в пункт В на 27 мин позже, чем второй в пункт А. Найдите скорость каждого велосипедиста.
Решение
Пусть y — скорость первого велосипедиста (в км\ч) , x — скорость второго.
Через час встретились ⇒ (.
Так как время первого на 27 минут меньше ⇒
.
Составим систему:

Ответ: 15 и 12.
Задание №23
Постройте график функции:
y=∣x∣x−∣x∣−6x,
и определите, при каких значениях а прямая y = а имеет с графиком ровно две общие точки.
Решение

Построим график функции. С учетом графика видно, что две точки пересечения будут только в том случае, когда прямая пройдет через одну из вершин парабол. Тогда: a=6,25 и a=-12,25.
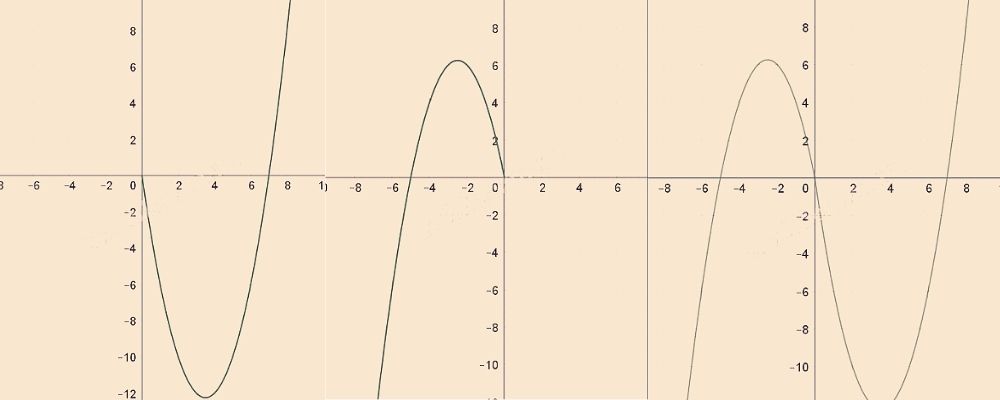
Ответ: 6,25 ; -12,25.
Задание №24

Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найти длины оснований этой трапеции.
Решение
- BC=x ⇒ MN-средняя линия , то BC+AD=2MN AD = 2MN — BC = 20-x.
- BK –высота и BH = HK = y ⇒

Ответ: 5, 15.
Задание №25
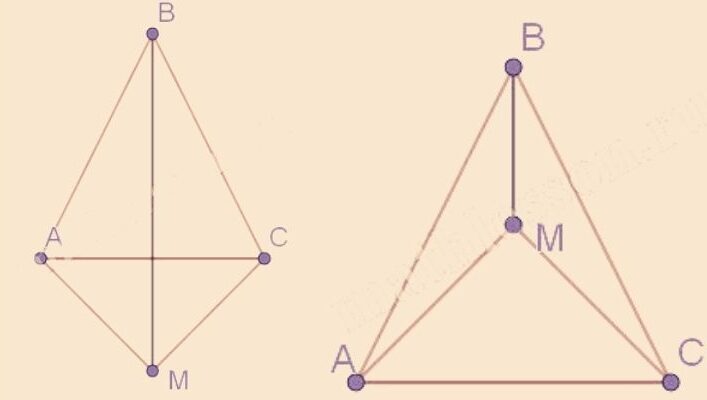
В равнобедренном треугольнике АВС из концов основания АС проведены прямые, которые составляют с основанием равные углы и пересекаются в точке М. Докажите равенство треугольников АВМ и ВСМ.
Решение
- –равнобедренный , тогда AM = MC.
- Треугольник ABC — равнобедренный, следовательно, AB = BC.
- BM — общая, следовательно, треугольники равны по трем сторонам.
Ответ: доказано.
Задание №26

В выпуклом четырехугольнике ABCD отрезок СМ, соединяющий вершину С с точкой М, расположенной на стороне AD, пересекает диагональ BD в точке К. Известно, что СК : КМ = 2 : 1, CD : DК = 5 : 3 и ∠АВС + ∠ACD = 180º. Найдите отношение стороны АВ и диагонали АС.
Решение

Ответ: 5/9.
