Решение варианта №225 ОГЭ Ларин по математике

Задание №01

На рисунке изображена схема метро города N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Всего в метрополитене города N есть три станции, от которых тоннель ведёт только в одну сторону – это станции Дальняя, Верхняя и Звёздная. Антон живёт недалеко от станции Надежда.Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других каких‐либо символов.

Смотреть решение

Задание №02

Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяжённостью 12,4 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 400 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?

Задание №03

Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь S(в км²), если длина кольцевой ветки равна 40 км. В ответе укажите значение выражения S*π.

Задание №04

Найдите расстояние (в км) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 17 км., расстояние от Звёздной до Смородиновой равно 10 км, а от Быстрой до Хоккейной – 12 км. Все расстояния даны по железной дороге.

Задание №05

Решение

Ответ: -4999,96.

Задание №07. Решение варианта №225 ОГЭ

На координатной прямой отмечены числа и a b.

Какое из приведённых утверждений всегда верно?

1. $$-b(a-b)<0$$
2. $$a²b(|a|-|b|)>0$$
3. $$-a(2a+b)>0$$
4. $$-ab(-a-b)>0$$

Решение

Ответ: 3.

Задание №08

Найдите значение выражение:

Решение​

Ответ: 27.

Задание №09. Решение варианта №225 ОГЭ Ларин по математике

Решите уравнение:−(−x−5)−2(−3x−7) = 5−(−x2−5x)+7xЕсли корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение

−(−x−5)−2(−3x−7) = 5−(−x2−5x)+7x ⇔

x+5+6x+14 = 5+x2+5x+7x ⇔

$$x²+5x-14=0.$$

Получим: x1​+x2​ = −5,  x1​∗x2​ = −14 ⇒ x1​ = -7 x2 ​= 2.

Ответ: x1​ = -7 x2 ​= 2.

Задание №10

В урне 7 белых и 4 чёрных шара. Из урны вынули один шар и, не глядя, отложили в сторону. После этого из урны взяли ещё один шар. Он оказался белым. Найдите вероятность, что первый шар, отложенный в сторону, – тоже белый.

Решение

Ответ: 0,6.

Задание №11. Решение варианта №225 ОГЭ Ларин по математике

На рисунке изображены графики функций вида:

y=ax²+bx+c .

Пусть – дискриминант квадратного трёхчлена:

ax²+bx+c .

Установите соответствие между графиками b  знаками  с и D.

Решение

Учтем, что если D < 0, то у графика нет пересечений с осью Ох, D > 0 — два пересечения. Если с > 0, то ось Оу пересекает над Ох, если с < 0, то под Ох. Тогда:

А) D > 0, c < 0 — 2

Б) D < 0, c > 0 — 3

В) D > 0, c > 0 — 4

Ответ: 234.

Задание №12. Решение варианта №225 ОГЭ Ларин по математике

Найдите сумму всех натуральных чётных двузначных чисел, делящихся на 3.

Решение

• 1 вариант решения:

12+18+24+30+36+42+48+54+60+66+72+78+84+90+96=810

12+18=30+24=54+30=84+36=120+42=162+48=210+54=264+60=324+66=390+72=462+78=540+84=624+90=714+96 = 810.

• 2 вариант решения:

Первое натуральное четное двузначное число, делящееся на 3: 12, последнее: 96. Следующее, получим путем прибавления к данному 6 и т.д. То есть имеем арифметическую прогрессию:

a1​=12, an​=96, d=6.

Найдем n:

$$96=12+6(n-1)\iff$$n=15.

Сумма первых 15 членов:

S = 15*(12 + 69)/2 = 810.

Ответ: 810.

Задание №13

Найдите значение выражения:

при x = 7 − 5√29​, y = 3 − √29.​

Решение

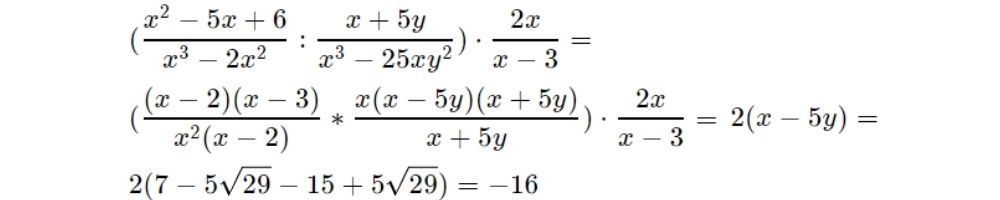
Ответ: -16.

Задание №14. Решение варианта №225 ОГЭ Ларин по математике

Длина биссектрисы треугольника, проведённой к стороне длиной a, равна:где b и с – длины сторон треугольника, α угол, противолежащий стороне длиной a. Пользуясь этой формулой, найдите b , если cosα/2 = 0,7, c = 5, l_a = 2,625.

Решение

Подставим значения:

2,625 = (2∗b∗5∗0,7)/(b+5) ​⇔

2*5/8 ​= 7b/(b+5) ​⇔

21/8 ​= 7b(b+5) ​⇔

$$21b+105=56b\iff$$b=3.

Ответ: 3.

Задание №15. Решение варианта №225 ОГЭ

Укажите решение системы неравенств:

Решение

Задание №16

Задание №18

Найдите площадь прямоугольной трапеции, одна из боковых сторон которой равна 7, а радиус окружности, вписанной в эту трапецию, равен 3.

Решение

Так как ​AB = h = 2r​, то из условия ​CD = 7.​

​h​ — высота трапеции

​2r = h = 6​ — видно из рисунка.

​AB+CD = BC+AD​ — это так как окружность вписана  в четырехугольник.

​S = AD+BC2∗h = 6+72∗6 = 39.

Ответ: 39.

Задание №19. Решение варианта №225 ОГЭ Ларин по математике

Найдите площадь квадрата, изображённого на рисунке.

Решение

По теореме Пифагора:

c = √((8−0)²+(2−0)²) =68 ⇒

площадь: $$S=c²=68.$$

Ответ: 68.

Задание №20. Решение варианта №225 ОГЭ Ларин

Какие из следующих утверждений равны?

1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2. Если диагонали четырёхугольника перпендикулярны и равны 3 и 5, то площадь этого четырёхугольника равна 7,5.
3. Площадь трапеции равна половине произведения средней линии и высоты этой трапеции.

Решение

1. верно, 1 признак подобия.
2. верно, т.к. если диагонали четырёхугольника перпендикулярны, то площадь будет равна половине произведения диагоналей.
3. неверно, т.к. площадь трапеции равна  произведению средней линии и высоты этой трапеции.

Ответ: 1, 2.

Задание №21. Решение варианта №225 ОГЭ Ларин по математике

Решите неравенство:

Решение

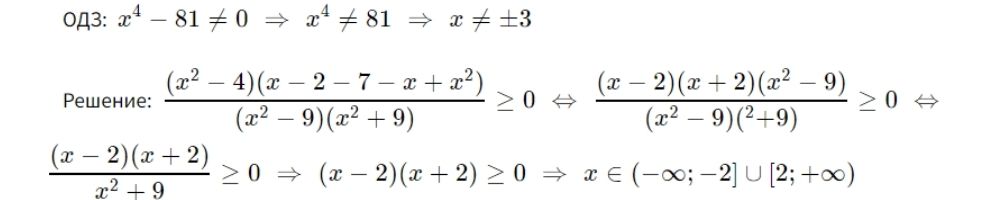
С учетом ОДЗ: x∈(−∞;−3)∪(−3;−2]∪[2;3)∪(3;+∞)

Ответ: x∈(−∞;−3)∪(−3;−2]∪[2;3)∪(3;+∞).

Задание №22

В солёную воду с содержанием соли 5% добавили 1 кг солёной воды с содержанием соли 10% и тщательно перемешали. Затем в полученную смесь добавили 2 кг солёной воды с содержанием соли 15%. Далее выпарили всю воду. Получилось 750 грамм соли. Сколько кг солёной воды было первоначально? Все процентные содержания соли даны по массе.

Задание №23. Решение варианта №225 ОГЭ Ларин по математике

Задание №24

В окружность радиуса 3 вписана равнобедренная трапеция с углом при основании 45 и высотой , равной √2 . Найдите площадь этой трапеции.

Задание №25

Дан треугольник ABC . На сторонах AB и BC построены внешним образом квадраты ABMN и BCPQ . Докажите, что центры этих квадратов и середины отрезков MQ и AC образуют квадрат.

Задание №26

Известно, $$\angle A=\; 24º$$, $$\angle B=81º$$ – внутренние углы треугольника ABC. O – такая точка внутри треугольника, что $$\angle OAB=15º$$, $$\angle OBA=69º$$. Найдите градусную меру угла OCA.

Решение

Ответ: 57º.

Видео: Разбор Варианта ОГЭ Ларина №225