Contents
- 1 Задание 1. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
- 2 Задание 2
- 3 Задание 3
- 4 Задание 4. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
- 5 Задание 5. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
- 6 Задание 6
- 7 Задание 7. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
- 8 Задание 8
- 9 Задание 9. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
- 10 Задание 10
- 11 Задание 11
- 12 Задание 12
- 13 Задание 13
- 14 Задание 14. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
- 15 Задание 15
- 16 Задание 16
- 17 Задание 17
- 18 Задание 18
- 19 Задание 19
- 20 Видео решение задания с 1 по 15 (Тренировочная работа 1 (профиль)по математике Статград 20.09.2018)
- 21 Видео решение задания с 16 по 19 (Тренировочная работа 1 (профиль)по математике Статград 20.09.2018)
Задание 1. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
На бензоколонке один литр бензина стоит 35 руб. 60 коп. Водитель залил в бак 30 литров бензина и взял бутылку воды за 35 рублей. Сколько рублей сдачи он получит с 1500 рублей?
Решение
Ответ: 397.
Задание 2
На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 8 августа. Ответ дайте в градусах Цельсия.

Решение
Из графика видно, что наибольшая температура воздуха 8 августа составила 33 градуса Цельсия.
Ответ: 33.
Задание 3
На клетчатой бумаге с размером клетки 1*1 изображён параллелограмм. Найдите длину его меньшей диагонали.
Решение

Проведем дополнительные построения, как показано на рисунке.
Найдём длину диагонали по теореме Пифагора:
BD = √(36+64) = 10.
Ответ: 10.
Задание 4. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
Решение
По условию, диаметр подшипника будет лежать в пределах от 75,99 до 76,01 мм с вероятностью 0,983.
Поэтому искомая вероятность противоположного события равна^
1 − 0,983 = 0,017.
Ответ: 0,017.
Задание 5. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
Найдите корень уравнения:
1/(12x — 11) = 1/4
Решение
Последовательно получаем:
1/(12x — 11) = 1/4 ⇔ 12x — 11 = 4 ⇔ 12x = 15 ⇔ x = 1.25.
Ответ: 1,25.
Задание 6
Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.

Решение

Ответ: 132.
Задание 7. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
На рисунке изображён график функции y = f(X), определённой на интервале (-3;10). Найдите количество точек, в которых производная функции f(X) равна 0.

Решение
Производная изображенной на рисунке функции f(x) равна нулю в точках экстремумов:
−2; −1; 0; 1; 2; 3; 6; 7; 8 и 9,6.
Производная равна 0 в 10 точках.
Ответ: 10.
Задание 8
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? Ответ выразите в сантиметрах.

Решение
Объем призмы равен произведению площади ее основания на высоту и выражается через сторону основания а и высоту Н формулой:
V = (√3a²/4)*H.
Поэтому: H = 4V/(√3a²/4),
значит, при увеличении стороны а в 2 раза знаменатель увеличится в 4 раза, то есть высота уменьшится в 4 раза и будет равна 4 см.
Ответ: 4.
Задание 9. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
Найдите значение выражения:
(√48 — √3 )* √12.
Решение
√48 = √(3*16) = √3√16 = 4√3
√12 = √(4*3) = √4*√3 = 2√3.
Следовательно:
(√48 — √3)*√12 = (4√3 — √3)*2√3 = 3√3*2√3 = 18
Ответ: 18.
Задание 10
При нормальном падении света с длиной волны λ=650 нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол ф (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением dsinф=kλ. Под каким минимальным углом ф (в градусах) можно наблюдать третий максимум на решётке с периодом, не превосходящим 1950 нм?
Решение
Задача сводится к решению неравенства d ≤1950 нм на интервале φ ∈ (0º, 90º),
при заданных значениях длины волны света:
λ = 650 нм и номера максимума k = 3:

Ответ: 90.
Задание 11
От пристани A к пристани B, расстояние между которыми равно 182 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью, на 1 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым. Ответ дайте в км/ч.
Решение

Ответ: 14.
Задание 12
Найдите наименьшее значение функции:
 на отрезке [-27;-25].
на отрезке [-27;-25].
Решение
Найдем производную заданной функции:

Наименьшим значением функции на отрезке [−27; −25] является
Ответ: 0.
Задание 13
a)Решите уравнение:

б) Найдите все корни этого уравнения, принадлежащие отрезку: [-7π/2;-5π/2]
Решение
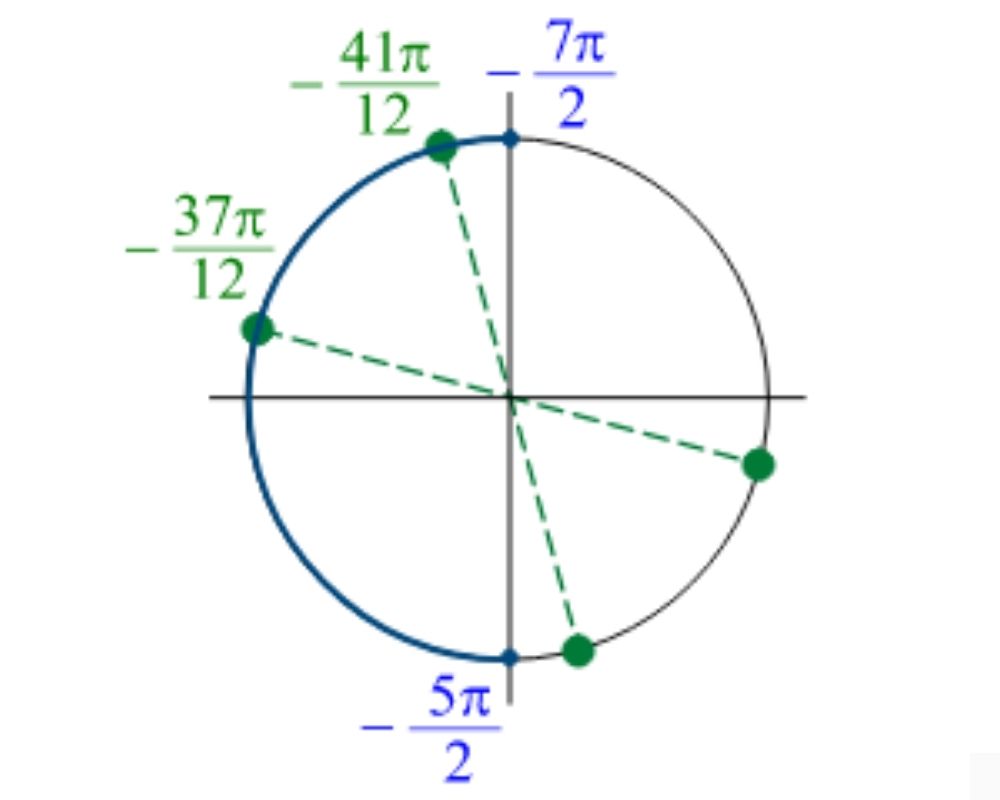


Ответ:
Задание 14. Тренировочная работа 1 (профиль)по математике Статград 20.09.2018
В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD со стороной 6. Противоположные боковые рёбра пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость а , параллельная ребру MC.
- а) Докажите, что сечение плоскостью а пирамиды MABC является параллелограммом.
- б) Найдите площадь сечения пирамиды MABC плоскостью а.
Решение
- а) Пусть точка Q — середина ребра MA, а точка K — середина ребра MB. Плоскость α пересекает плоскость BMC по отрезку KL. Так как плоскость α параллельна ребру MC, то KL || MC, следовательно, KL — средняя линия треугольника AMC, а L — середина ВС. Плоскость α проходит через QK — среднюю линию треугольника MAB, и, следовательно, параллельна AB. Таким образом, пересекает плоскость основания по прямой параллельной AB — средней линии треугольника АВС и проходит через точку O — середину отрезка AC. Значит, сечение — четырёхугольник QKLO, в котором стороны QK и LO параллельны отрезку AB и равны его половине. Значит, QKLO —параллелограмм.

- б) Отметим точку F — середину отрезка QK и рассмотрим плоскость MOF. Прямая QK перпендикулярна прямым FM и MO, следовательно, она перпендикулярна плоскости MFO, поэтому она перпендикулярна отрезку OF. Таким образом, отрезок OF служит высотой параллелограмма QKLO. Сечение пирамиды MABCD плоскостью MOF — равнобедренный треугольник NMG. Отрезок OF является медианой прямоугольного треугольника MOG, проведённой к его гипотенузе, поэтому OF = ½MG.
По условию треугольник AMC прямоугольный и равнобедренный, поэтому:

Ответ: 9√3/2.
Задание 15
Решите неравенство:

Решение
Решим неравенство методом интервалов:
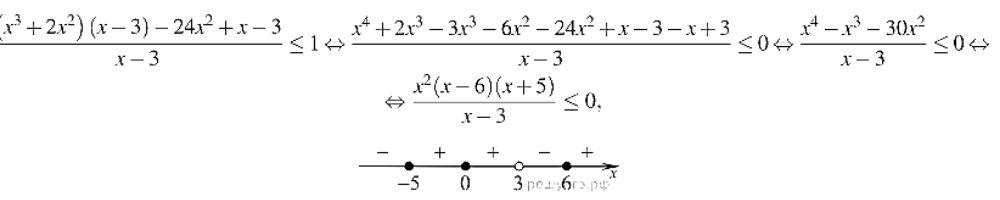
откуда:
x ≤ -5, x = 0 и 3 < x ≤ 6.
Ответ: (-∞; — 5]; {0}; (3; 6].
Задание 16
Две окружности касаются внешним образом в точке C. Прямая касается меньшей окружности в точке A, а большей — в точке B, отличной от A. Прямая AC вторично пересекает большую окружность в точке D, прямая BC вторично пересекает меньшую окружность в точке E.
- а) Докажите, что прямая AE параллельна прямой BD.
- б) Пусть L — отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 5.
Решение
а) Пусть общая касательная к данным окружностям, проведённая через точку C, пересекает общую касательную AB в точке M. Тогда MA = MC = MB, то есть медиана CM треугольника ABC равна половине стороны AB.
Значит, ∠ACB = 90º.
Тогда ∠ACE = 90º, поэтому AE — диаметр меньшей окружности. Следовательно, прямая AE перпендикулярна прямой AB.
Аналогично докажем, что прямая BD перпендикулярна прямой AB. Прямые AE и BD перпендикулярны одной и той же прямой AB, значит, они параллельны.
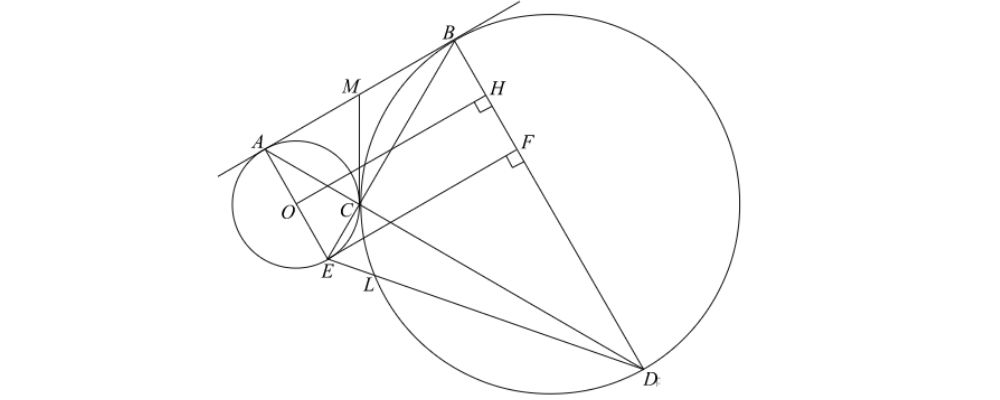
б) Пусть радиусы окружностей равны r и R, где r < R. Опустим перпендикуляр OH из центра O меньшей окружности на диаметр BD большей. Тогда:
OH² = (R + r)² — (R — r)² = 4rR.
Опустим перпендикуляр EF из точки E на BD. Тогда:

Ответ: (8√19)/19.
Задание 17
По бизнес-плану предполагается вложить в четырёхлетний проект целое число млн рублей. По итогам каждого года планируется прирост средств вкладчика на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект.
Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 15 млн рублей в первый и второй годы, а также по 10 млн в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика к началу третьего года станет больше 110 млн, а к концу проекта — больше 190 млн рублей.
Решение
Пусть S млн — первоначальные вложения. К началу 2-го года получится 1,2S + 15 млн, а к началу 3-го года:
1,2(1.2S + 15) + 15 = 1.44S + 33.
По условию^
1.44S + 33 > 110, откуда:
S > 77/1.44 = 53.4
К началу 4-го года имеем:
1.2(1.44S + 33) + 10, а в конце проекта:
1.2(1.2(1.44S + 33) + 10) + 10 = 2,0736S + 47.52 + 22 = 2,0736S + 69,52
По условию:
2.0736S + 69.52 >190, откуда S > 120.48/2.0736 = 58.1
А значит, минимальное возможное целое значение: S = 59.
Ответ: 59 млн. рублей.
Задание 18
Найдите все значения a, при которых уравнение:
(x² + 2x + 2a)² = 5x4 + 5(x + a)²
имеет единственное решение на отрезке [0; 2].
Решение

Ответ: -1/8; (0; 6].
Задание 19
Пусть K (n) обозначает сумму квадратов всех цифр натурального числа n.
- а) Существует ли такое трёхзначное число n, что K (n) =171?
- б) Существует ли такое трёхзначное число n, что K (n)) =172?
- в) Какое наименьшее значение может принимать выражение 4K(n)-n , если n — трёхзначное число?
Решение
а) Такое число существует. Например, для числа n = 399 имеем 3² + 9² + 9² = 171.
б) Заметим, что для любого целого числа k число k2 либо делится на 4, если k чётно, либо даёт при делении на 4 остаток 1, если k нечётно. Значит, сумма квадратов всех цифр произвольного трёхзначного числа n может делиться на 4, только если квадрат каждой из его цифр делится на 4, то есть когда все его цифры чётны.
Следовательно, если K(n) = 172 = 4*43 то все цифры числа n чётны и либо:
K(n) = 82 + 82 + 82 = 192, либо K(n) = 82 + 82 + 62 = 164. Значит, искомого числа n не существует.

Ответ: а) Да; б) нет; в) −582.

