Contents
- 1 Задание №01
- 2 Задание №02. Решение варианта №1 по математике 9 класс 03.10.2019 Статград ОГЭ по математике.
- 3 Задание №03. Решение от 03.10.2019 Статград ОГЭ по математике
- 4 Задание №04
- 5 Задание №05. Решение от 03.10.2019 Статград ОГЭ по математике
- 6 Задание №06. Решение от 03.10.2019 Статград ОГЭ по математике
- 7 Задание №07
- 8 Задание №08. Решение от 03.10.2019 Статград ОГЭ по математике
- 9 Задание №09. Решение от 03.10.2019 Статград ОГЭ по математике
- 10 Задание №10. Решение от 03.10.2019 Статград ОГЭ по математике
- 11 Задание №11. Решение от 03.10.2019 Статград ОГЭ по математике
- 12 Задание №12. Решение от 03.10.2019 Статград ОГЭ по математике
- 13 Задание №13
- 14 Задание №14
- 15 Задание №15. Решение от 03.10.2019 Статград ОГЭ по математике
- 16 Задание №16
- 17 Задание №17
- 18 Задание №18
- 19 Задание №19
- 20 Задание №20. Решение от 03.10.2019 Статград ОГЭ по математике
- 21 Задание №21. Решение от 03.10.2019 Статград ОГЭ по математике
- 22 Задание №22. Решение от 03.10.2019 Статград ОГЭ по математике
- 23 Задание №23. Решение от 03.10.2019 Статград ОГЭ по математике
- 24 Задание №24
- 25 Задание №25. Решение от 03.10.2019 Статград ОГЭ по математике
- 26 Задание №26. Решение от 03.10.2019 Статград ОГЭ по математике
- 27 Видео: Разбор варианта ОГЭ Статград от 3 октября 2019
Задание №01
На плане изображено домохозяйство по адресу с. Кондратьево, 2-й Прудовой пер, д. 7 (сторона каждой клетки на плане равна 1 м).
Участок имеет прямоугольную форму. Выезд и въезд осуществляется через единственные ворота. При входе на участок слева от ворот находится сарай, а справа гараж.
Площадь, занятая сараем, равна 16 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеются теплица и две круглые клумбы, расположенные на территории огорода(огород отмечен на плане цифрой 5).
Все дорожки внутри участка имеют ширину 0,5 м и вымощены тротуарной плиткой размером 0,5 м 0,5 м´. Между сараем и гаражом имеется площадка, вымощенная той же плиткой и они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.

Решение
При входе на участок слева от ворот находится сарай, а справа гараж. Значит, сарай отмечен цифрой 2, а гараж — цифрой 1. Жилой дом находится в глубине территории, следовательно, жилой дом отмечен цифрой 3.
Помимо гаража, жилого дома и сарая, на участке имеются теплица и две круглые клумбы, расположенные на территории огорода (огород отмечен на плане цифрой 5). Следовательно, теплица отмечена цифрой 4.
| жилой дом | теплица | гараж | сарай |
| 3 | 4 | 1 | 2 |
Ответ: 3, 4, 1, 2.
Задание №02. Решение варианта №1 по математике 9 класс 03.10.2019 Статград ОГЭ по математике.
Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось,
чтобы выложить все дорожки и площадку перед гаражом? Текстовые задачи(лёгкий уровень)
Решение
Поскольку одна плитка имеет площадь 0,25 м2, для площадки перед гаражом понадобится:
4*4*16 = 256 плиток.
Для того чтобы выложить все дорожки, понадобится ещё 40 плиток. Значит, всего необходимо 296 плиток.
Теперь найдём, сколько упаковок плитки понадобилось: 296/5 = 59,2.
Следовательно, чтобы выложить все дорожки и площадку перед гаражом понадобится 60 упаковок плитки.
Ответ: 60.
Задание №03. Решение от 03.10.2019 Статград ОГЭ по математике
Вычислите примерно площадь, которую занимают две клумбы вместе. Число π возьмите равным 3,14.
Текстовые задачи(лёгкий уровень) Площади фигур
Решение
Площадь меньшей клумбы равна:
S = πR1² = 3.14*2² = 12.56 м2.
Площадь большей клумбы равна:
S = πR2² = 3.14*3² = 28.26 м2.
Таким образом, площадь, которую занимают две клумбы вместе, равна 12,56 + 28,26 = 40,82 м2.
Ответ: 40,82.
Задание №04
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Текстовые задачи(лёгкий уровень). Практические задачи. Площади фигур
Решение
S = 2*4 + 8*8 = 72 м2.
Ответ: 72 м2.
Задание №05. Решение от 03.10.2019 Статград ОГЭ по математике
Хозяин участка хочет сделать пристройку к дому. Для этого он планирует купить 12 тонн силикатного кирпича.
Один кирпич весит 3 кг. Цена кирпича и условия доставки всей покупки приведены в таблице ниже.
| Поставщик | Цена кирпича (руб. за шт.) | Стоимость доставки (руб.) до 15 тонн (руб.) | Специальные условия |
|---|---|---|---|
| А | 12,48 | 8000 | Доставка бесплатно, если сумма заказа превышает 50 000 руб. |
| Б | 14,68 | 5000 | Доставка со скидкой 50 %, если сумма заказа превышает 55 000 руб. |
Во сколько рублей обойдётся наиболее дешёвый вариант?
Решение
Всего необходимо купить 12000/3 = 4000 кирпичей.
При покупке у поставщика А цена кирпича составит 4000*12,48 = 49920 руб. Значит, общая сумма заказа равна 49920 + 8000 = 57920 руб.
При покупке у поставщика Б цена кирпича составит 4000*14,68 = 58720 руб. Значит, общая сумма заказа равна 58720 + 2500 = 61220 руб.
Ответ: 57 920.
Задание №06. Решение от 03.10.2019 Статград ОГЭ по математике
Найдите значение выражения:
-0.7*(-10)²+90
Выражения Числовые выражения
Решение
Последовательно получаем:
-0.7*(-10)²+90 = 90 — 70 = 20.
Ответ: 20.
Задание №07
На координатной прямой точки A, B, C и D соответствуют числам 0,0137; 0,103; 0,03; 0,021.

Какой точке соответствует число 0,03?
1) A 2) B 3) C 4) D
Сравнение чисел
Решение
Заметим, что
0,0137 < 0.021 <0.03 < 0.103.
Следовательно, числу 0,03 соответствует третья слева точка то есть точка C.
Ответ: 3.
Задание №08. Решение от 03.10.2019 Статград ОГЭ по математике
Найдите значение выражения^
(√11-3)(∼11+3).
Решение
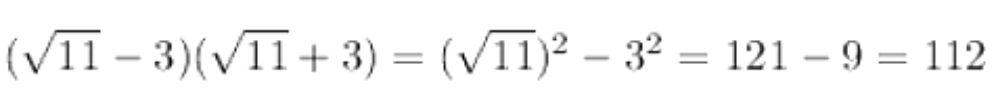
Ответ: 112.
Задание №09. Решение от 03.10.2019 Статград ОГЭ по математике
Решите уравнение:
(-5x + 3)(-x + 6) = 0.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решение
(-5x+3)(-x+6) = 0,
5x²-30x-3x+18 = 0,
5x²-33x+18 = 0,
D = 1089-4*5*18 = 729,
x1 = (33+27)/10 = 6,
x2 = (33-27)/10 = 0.6.
Ответ: 0,6.
Задание №10. Решение от 03.10.2019 Статград ОГЭ по математике
У бабушки 20 чашек: 12 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку.
Найдите вероятность того, что это будет чашка с синими цветами.
Теория вероятностей
Решение
Количество синих чашек, значит m = 20–12 = 8.
Вероятность того, что бабушка нальет в синюю равна:
P = 8/20 = 0,4.
Ответ: 0,4.
Задание №11. Решение от 03.10.2019 Статград ОГЭ по математике
Установите соответствие между графиками функций и формулами, которые их задают.

Исследование функции
Решение
Определим вид графика каждой из функций.
1) y = x + 2 — уравнение параболы.
2) y = -2/x — уравнение гиперболы.
3) y = 2x — уравнение прямой.
Тем самым найдено соответствие:
A — 1, Б — 3, В — 2.
| А | Б | В |
| 1 | 3 | 2 |
Ответ: 132.
Задание №12. Решение от 03.10.2019 Статград ОГЭ по математике
Последовательность (cn ) задана условиями:
C1 = 6 Cn+1 = Cn + 2.
Найдите с7 .
Арифметическая прогрессия
Решение
Будем вычислять последовательно:
C2 = 8; C3 = 12; C4 = 12; C5 = 14; C6 = 16; C7 = 18.
Ответ: 18.
Задание №13
Найдите значение выражения:
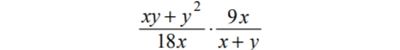
при:
x = −9,6,
y = −0,4.
Выражения Рациональные выражения
Решение
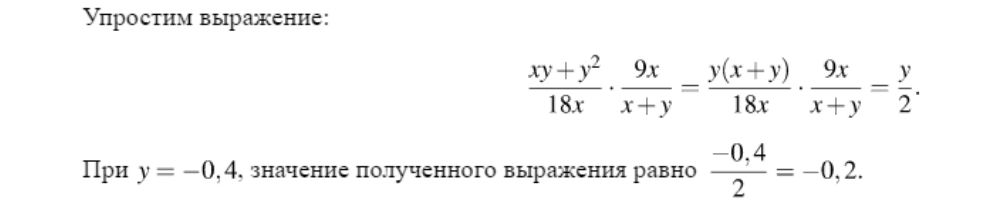
Ответ: −0,2.
Задание №14
Площадь четырёхугольника можно вычислить по формуле:
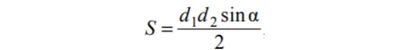
где d1 и d2 — длины диагоналей четырёхугольника,
α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2 , если d =11, sinα = 1/8, a S = 8,25.
Работа с формулами
Решение

Ответ: 15.
Задание №15. Решение от 03.10.2019 Статград ОГЭ по математике
Укажите решение системы неравенств:
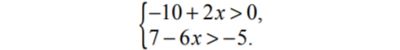
- нет решений.
- (5; + ∞).
- ( 2; 5).
- ( — ∞; 2).
Системы неравенств
Решение
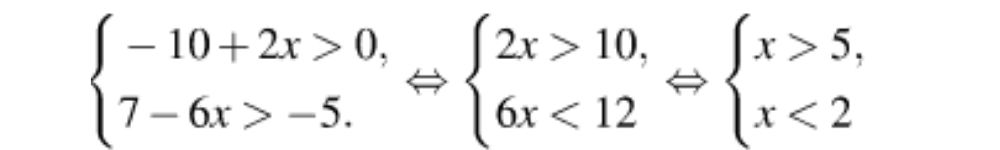
Ответ: 1.
Задание №16
В треугольнике ABC известно, что угол BAC=64 , AD — биссектриса. Найдите угол BAD.
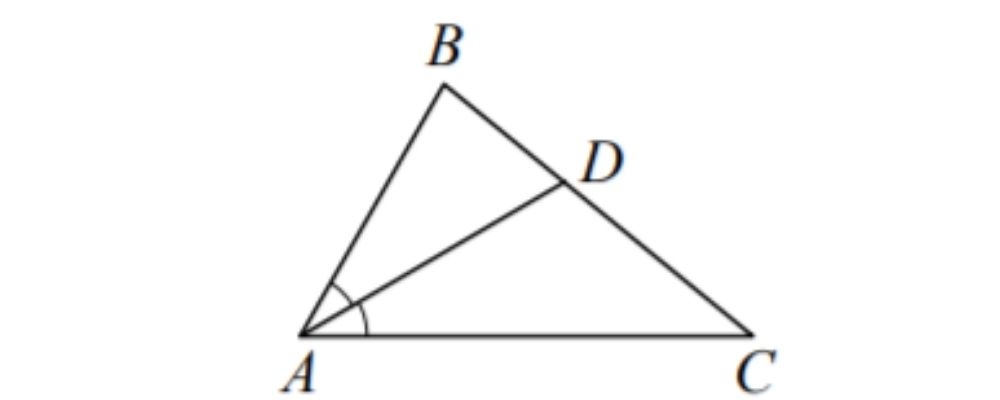
Ответ дайте в градусах.
Планиметрия (легкий уровень) Треугольник
Решение
Задание №17
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72° . Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC . Ответ дайте в градусах.
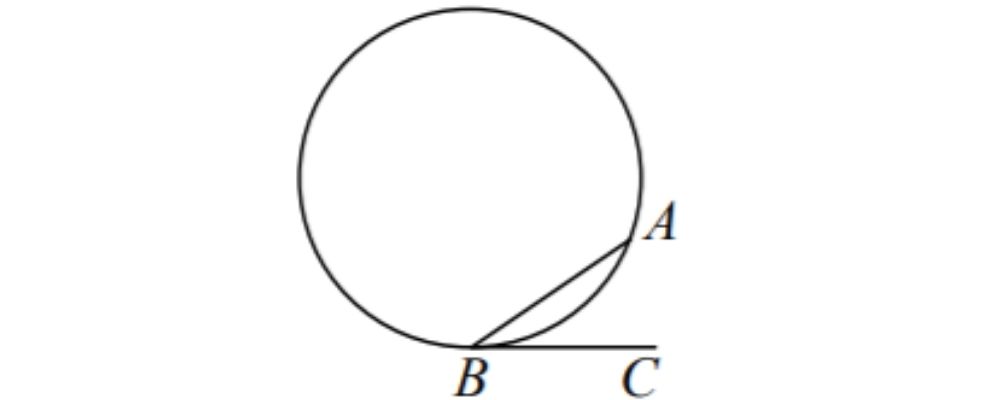
Планиметрия (легкий уровень) Окружность
Решение
Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой, следовательно:
∠АВС = 72/2 = 36°.
Ответ: 36°
Задание №18
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 10 и 11.
Найдите длину основания BC .
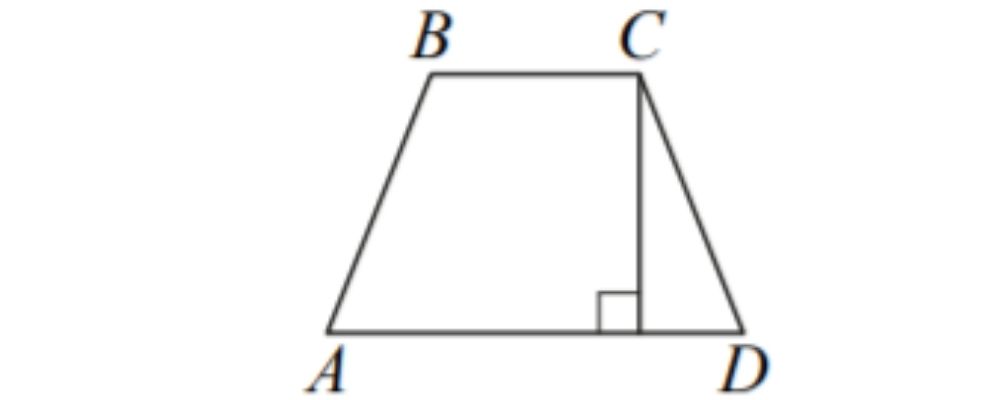
Планиметрия (легкий уровень) Трапеция
Решение
Проведем высоту BH2. Так как данная трапеция равнобедренная, отрезки AH2 = H1D = 10.
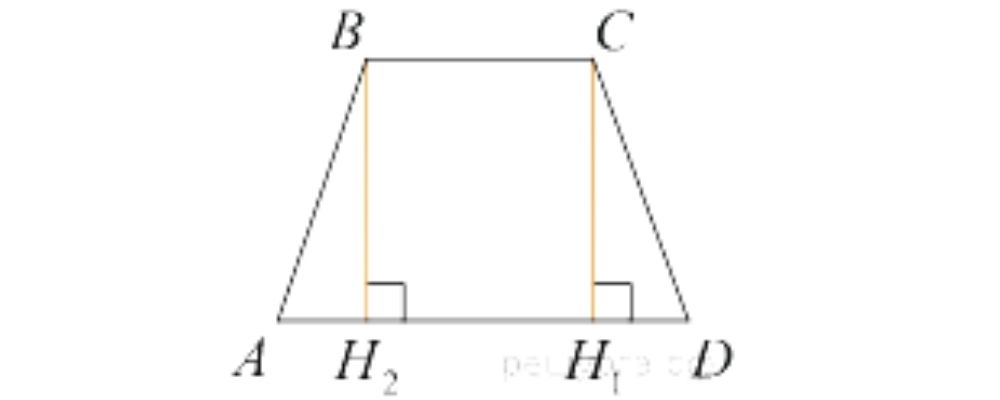
Заметим, что , AH1 = AH2 + H2H1 = 11.
H2H1 = 9 — AH2 = 11 — 10 = 1.
а так как BC и H1H2 параллельны, а BH2 и CH1 перпендикулярны к BC, то BC = H2H1 = 1.
Ответ: 1.
Задание №19
На клетчатой бумаге с размером клетки 1*1 изображён параллелограмм. Найдите его площадь.

Планиметрия (легкий уровень) Площади фигур
Решение
Площадь параллелограмма равна произведению основания на проведенную к нему высоту.
Следовательно S = 6*3 = 18.
Ответ: 18.
Задание №20. Решение от 03.10.2019 Статград ОГЭ по математике
Какое из следующих утверждений верно?
1) Треугольник со сторонами 1, 2, 4 существует.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Две прямые, перпендикулярные третьей прямой, перпендикулярны.
В ответе запишите номер выбранного утверждения.
Планиметрия(теория)
Решение
1. Треугольник со сторонами 1, 2, 4 существует — неверно, так как по свойству треугольника ни одна из сторон не должна быть больше суммы двух других сторон, в данном же случае 4 > 1 + 2.
2. Диагонали ромба точкой пересечения делятся пополам — верно.
3. Две прямые, перпендикулярные третьей прямой, перпендикулярны — неверно, две прямые, перпендикулярные третьей прямой, параллельны.
Ответ: 2.
Задание №21. Решение от 03.10.2019 Статград ОГЭ по математике
Решите неравенство:
(x — 9)² < √2(x — 9).
Рациональные неравенства
Решение
(x — 9)² < √2(x — 9) ⇔ (x — 9) (x — 9 — √2) < 0 ⇔ 9 < x < 9 + √2.
Ответ: (9; 9 + √2).
Задание №22. Решение от 03.10.2019 Статград ОГЭ по математике
Баржа прошла по течению реки 72 км и, повернув обратно, прошла ещё 54 км, затратив на весь путь 9 часов.
Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Текстовые задачи (средний уровень) Задачи на движение
Решение
- Пусть Х — скорость баржи;
- 72/(х+5)+54/(х-5) = 9;
- Умножим на (х+5)(х-5);
- 72(х-5)+54(х+5) = 9(х+5)(х-5);
- 72х-360+54х+270 = 9(х-25);
- 126х-90 = 9х-225;
- 9х-126х-135 = 0;
- х-14х-15 = 0;
- D = (-14) — 41(-15) = 196 + 60 = 256;
- x1 = (14 — 256)/(21) = (14 — 16)/2 = -2/2 = -1;
- x2 = (14 + 256)/(21) = (14 + 16)/2 = 30/2 =15км/час.
Ответ: скорость баржи 15км/час.
Задание №23. Решение от 03.10.2019 Статград ОГЭ по математике
Постройте график функции:
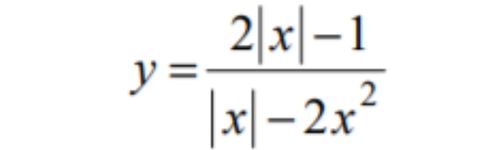
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Построение графиков (параметр)
Решение
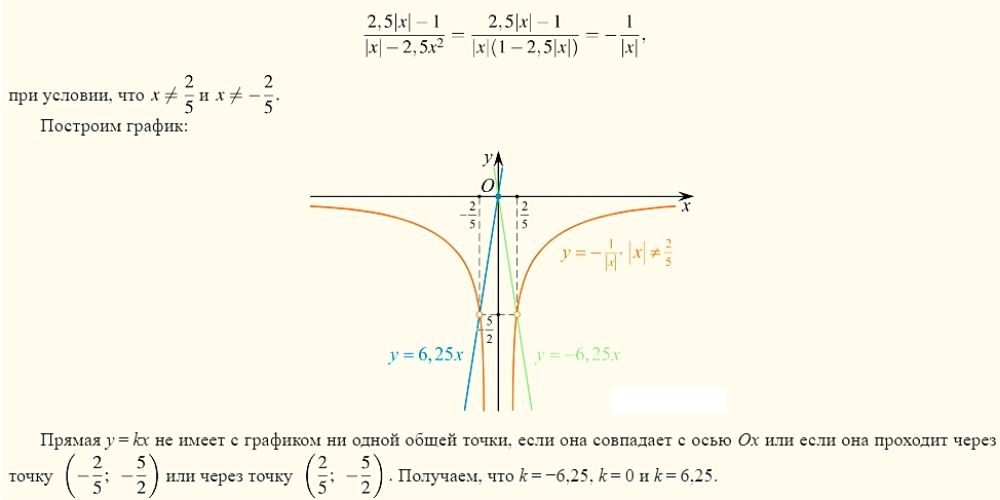
Ответ: −6,25; 0; 6,25.
Задание №24
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 34, а сторона BC в 2 раза меньше стороны AB.
Планиметрия (средний уровень)
Решение
Пусть сторона BC = x, тогда AB = 2x, так как она в 2 раза больше стороны BC по условию задачи. Рассмотрим четырехугольник CPKB, который вписан в окружность. Как известно, у такого четырехугольника сумма противоположных углов равна 180 градусов, то есть:
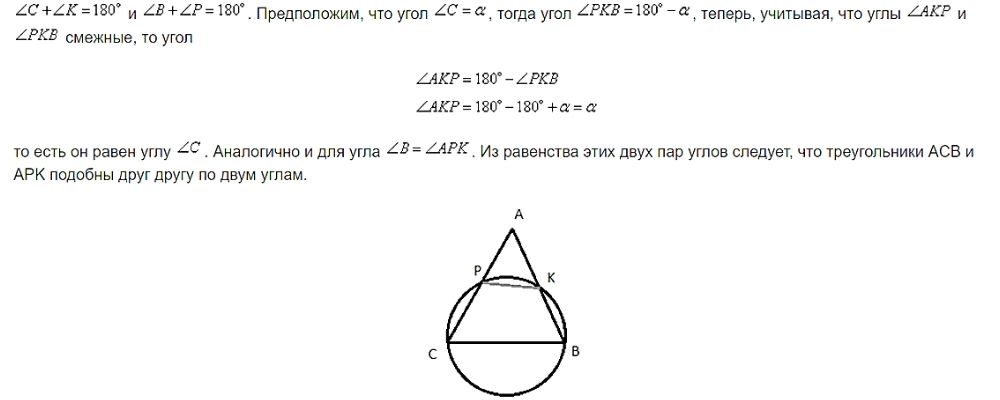
Для подобных треугольников можно записать следующее соотношение:
AB/AP = CB/KP,
откуда:
KP = CB*(AP/AB),
и подставляя числовые значения, имеем:
KP = 34 : 2 = 17
Ответ: 17.
Задание №25. Решение от 03.10.2019 Статград ОГЭ по математике
Внутри параллелограмма ABCD выбрали произвольную точку F . Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
Задачи на доказательство (геометрия)
Решение
Проведем в параллелограмме ABCD высоту MN, равную h, и проходящую через точку E. Пусть расстояние ME = x, тогда NE = h-x. Площадь параллелограмма можно вычислить как:
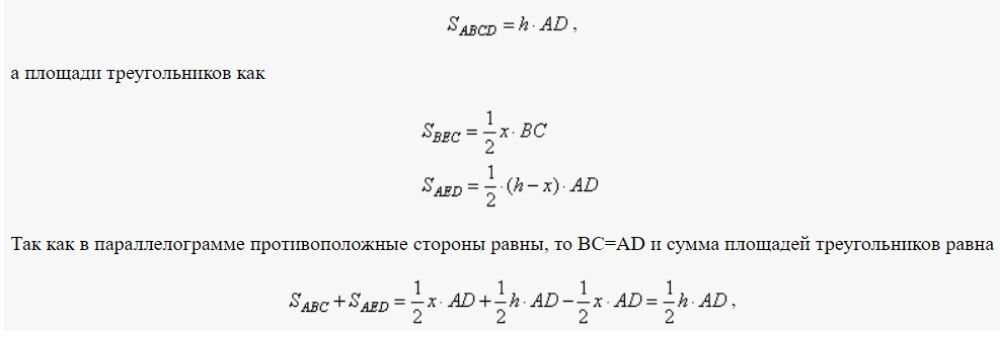
что в точности равно половине площади параллелограмма ABCD.
Утверждение доказано.
Задание №26. Решение от 03.10.2019 Статград ОГЭ по математике
Углы при одном из оснований трапеции равны 53° и 37°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 2. Найдите основания трапеции.
Планиметрия (сложный уровень)
Решение
По условию задания в трапеции ABCD углы при основании 53º и 37º, то есть,
∠A + ∠D = 53 + 37 = 90 градусов.
Продлим стороны AB и CD до их пересечения в точке F. Получим треугольник AFD с углом:
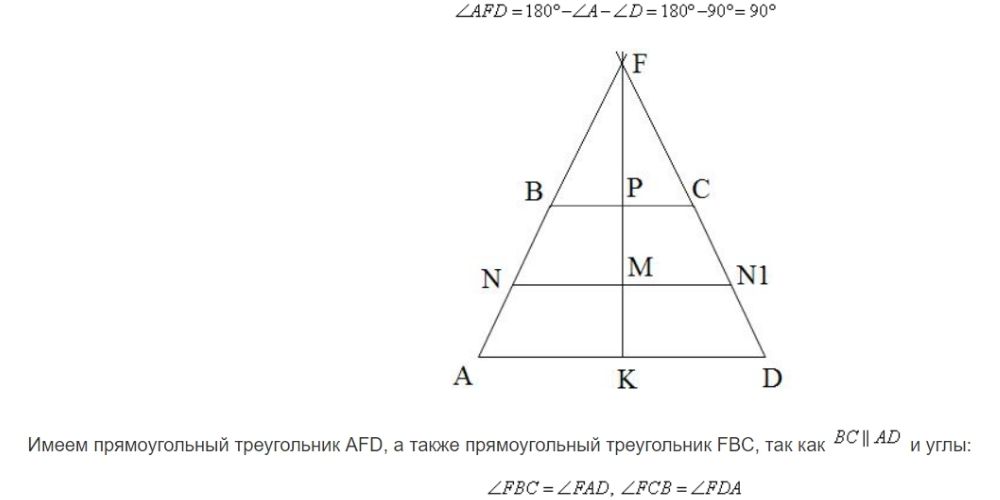
Имеем прямоугольный треугольник AFD, а также прямоугольный треугольник FBC, так как ![]() и углы:
и углы:
![]()
как соответственные при параллельных прямых. Пусть точка P – середина BC.
Учитывая, что угол F = 90º, имеем равные отрезки:
FP = BP = CP (как радиусы описанной окружности вокруг треугольника BFC).
Аналогично для точки K – середины отрезка AD, имеем:
FK = AK = KD.
По условию NN1 = 6 – средняя линия трапеции, значит, BC+AD=12 – в 2 раза больше средней линии. Следовательно, BP+AK=6. Далее, пусть FP=BP=x. Тогда FK=FP+PK=x+2 (PK=2 по условию задания).
Следовательно, AK = x+2. Получаем уравнение:
BP + AK = 6;
x + (x + 2) = 6;
2x = 4;
x = 2.
Следовательно:
- BP=2, AK=4;
- BC=2∙BP=4,
- AD=2∙AK=8.
Ответ: 4; 8.

Спасибо