Contents
- 1 Задание №01
- 2 Задание №02. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 3 Задание №03. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 4 Задание №04. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 5 Задание №05. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 6 Задание №06
- 7 Задание №07
- 8 Задание №08
- 9 Задание №09
- 10 Задание №10. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 11 Задание №11
- 12 Задание №12. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 13 Задание №13
- 14 Задание №14. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 15 Задание №15
- 16 Задание №16
- 17 Задание №17
- 18 Задание №18. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 19 Задание №19. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 20 Задание №20. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 21 Задание №21. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
- 22 Задание №22
- 23 Задание №23
- 24 Задание №24
- 25 Задание №25
- 26 Задание №26
- 27 Видео: Разбор Варианта ОГЭ Ларина №226 (№1-20) усложненная версия ОГЭ-2020
Задание №01
На схеме (см. рисунок) изображён план застройки участка. Въезд и выезд осуществляется через ворота.
При въезде на участок слева от ворот находится огород (на схеме отмечен цифрой 7). На его территории
находится подсобное помещение для сельскохозяйственного инвентаря (подсобка). Справа от ворот
находится сарай для кур и гусей, к которому примыкает выгульный вольер, обозначенный на схеме цифрой 5.
Рядом с вольером располагается водоём. От ворот до дальнего края участка проходит асфальтовый проезд,
заканчивающийся площадкой, также покрытой асфальтом. Рядом с площадкой находится мастерская
площадью 32 м2 и гараж, отмеченный на плане цифрой 3.
С другой стороны от площадки расположен жилой дом, окружённый газоном.

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме.
Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других каких‐либо символов.
| Объекты | Водоём | Мастерская | Подсобка | Сарай для птиц Цифры |
Решение
Задание №02. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
Найдите периметр (в метрах), который занимает огород (без учёта площади подсобного помещения для инвентаря).
Решение
Задание №03. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
Согласно санитарным нормам, в помещении на одном квадратном метре может располагаться не более 4 кур и 2 гусей.
Какое наибольшее количество гусей может поместиться в сарае для птиц, если необходимо, чтобы отношение количества кур к количеству гусей было 6:1.
Решение
32 — 5 = 27(м²) для гусей осталось.
27*2 = 54(гусей) максимум может поместиться.
Ответ: 54.
Задание №04. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
Найдите расстояние от подсобки до мастерской в метрах. Расстояние измеряйте между двумя ближайшими точками по прямой. В ответе укажите квадрат полученного значения.
Решение
Задание №05. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
| Тип лампы | Цена лампы, руб. | Мощность средняя, Вт. | Срок службы, часов | Стоимость электроэнергии руб/кВТ*ч |
| Накаливания | 19 | 40 | 1000 | 3,8 |
| Газоразрядные | 44 | 10 | 5000 | 3,8 |
| Светодиодные | 79 | 5 | 20000 | 3,8 |
Сколько рублей экономии при потреблении электроэнергии и сокращении числа заменяемых ламп получит хозяин за 1 год(365 дней), если 30 лампочек накаливания в жилом доме и 10 лампочек накаливания в других помещениях он заменит на газоразрядные лампы? Считайте, что в сутки каждая лампа горит 10 часов и лампы накаливания пришлось бы заменить за год 3 раза?
Решение
30+10 = 40 лампочек всего.
365·10 = 3650 часов будет гореть каждая лампа в течение года.
Лампы накаливания:
40·3 = 120 ламп накаливания нужно на год с учётом замены.
19·120 = 2280 руб на покупку ламп накаливания.
40·10 = 400 Вт потребляет одна лампа накаливания за 1 день.
400·40 = 16000 Вт = 16 кВт потребляют все лампы накаливания за 1 день.
3,8·16 = 60,8 руб ежедневные расходы на электроэнергию при использовании ламп накаливания.
60,8·365 = 22192 руб годовые расходы на электроэнергию при использовании ламп накаливания.
2280+22192 = 24472 руб всего годовые затраты при использовании ламп накаливания.
Газоразрядные лампы:
Срок службы 5000 ч говорит о том, что в течение первого года менять лампы не потребуется.
44·40 = 1760 руб затраты на покупку газоразрядных ламп.
10·10 = 100 Вт потребляет одна газоразрядная лампа за 1 день.
100·40 = 4000 Вт = 4 кВт потребляют все газоразрядные лампы за 1 день.
3,8·4 = 15,2 руб ежедневные расходы на электроэнергию при использовании газоразрядных ламп.
15,2·365 = 5548 руб годовые расходы на электроэнергию при использовании газоразрядных ламп.
1760+5548 = 7308 руб всего годовые затраты при использовании газоразрядных ламп.
Светодиодные лампы:
Срок службы 20000 ч говорит о том, что в течение первого года менять лампы не потребуется.
79·40 = 3160 руб затраты на покупку светодиодных ламп.
5·10 = 50 Вт потребляет одна светодиодная лампа за 1 день.
50·40 = 2000 Вт = 2 кВт потребляют все светодиодные лампы за 1 день.
3,8·2 = 7,6 руб ежедневные расходы на электроэнергию при использовании светодиодных ламп.
7,6·365 = 2274 руб годовые расходы на электроэнергию при использовании светодиодных ламп.
3160+2274 = 5934 руб всего годовые затраты при использовании светодиодных ламп.
При использовании светодиодных ламп хозяин сэкономит 24472-5934 = 18538 рублей. В последующие годы экономия будет ещё больше, так как светодиодные лампы требуют замены в 20 раз реже, чем лампы накаливания.
Задание №06
Найдите значение выражения:

Числовые выражения
Решение
Задание №07
Сравните числа:
a = √13 + 2√3 и b = √14 + √11/
Сравнение чисел
Решение

Ответ: a > b.
Задание №08
Найдите значение выражения:

Иррациональные выражения
Решение
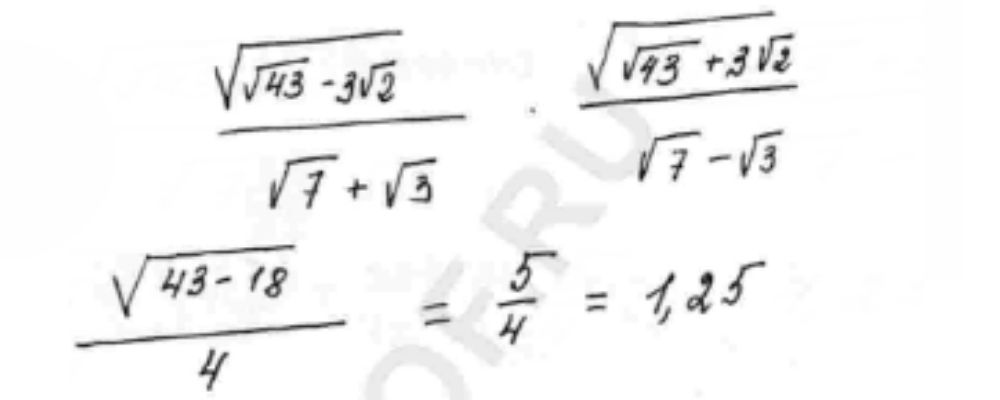
Ответ: 1,25.
Задание №09
Решите уравнение:

Если корней несколько, запишите их в ответ без пробелов и других дополнительных символов в порядке возрастания.
Простейшие уравнения Дробно-рациональные уравнения
Решение
Задание №10. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
В урне 4 белых и 9 чёрных шаров. Из урны вынимают сразу два шара. Найдите вероятность того, что оба шара будут белыми. Результат округлите до тысячных.
Теория вероятностей
Решение
Рб1 = 4/(4+9) = 4/13;
Условная вероятность что шар белый:
Р(б2/б1) = 3/12 = 1/4;
Р(б1б2) = Рб1 * Р(б2/б1) = 4/13 * 1/4 = 1/13 = 0,077.
Ответ: 0,077.
Задание №11
Установите соответствие между графиками функций и формулами, которые их задают.

В ответе укажите последовательность цифр, соответствующих графикам функций А, Б, В без пробелов и других дополнительных символов.
- y = 1/2x;
- y = -2/x;
- y = 2/x;
- y = -1/2x.
Исследование функции
Решение
Задание №12. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
В бесконечно убывающей геометрической прогрессии сумма первых четырёх членов равна 45, а сумма прогрессии равна 48. Найдите сумму пяти членов это прогрессии. В ответе запишите сумму полученных значений.
Геометрическая прогрессия
Решение
Задание №13
Найдите значение выражения:

при x = 31 — 5√37 y = 13 — 2√37.
Рациональные выражения
Решение
Задание №14. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике

Практические задачи Работа с формулами
Решение

Задание №15
Укажите решение системы неравенств:

Системы неравенств:
- (- ∞; -3]
- [- 4; ∞)
- [- 4; -3]
- [- 4; -3]∪{2}
Решение

Задание №16
В остроугольном треугольнике ABC угол A равен 34º. BD и CE – высоты, пересекающиеся в точке O . Найдите градусную меру угла BOE.
Планиметрия (легкий уровень) Треугольник
Решение

Ответ: 34º
Задание №17
В тупоугольном треугольнике ABC известно, что AC=BC , высота AH =7 , CH =24 . Найдите cos∠ACB .
Планиметрия (легкий уровень) Треугольник
Решение

Ответ: -0,96.
Задание №18. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
Площадь, периметр и средняя линия вписанной в окружность трапеции равны 192, 58 и 16 соответственно. Найдите диагональ этой трапеции.
Планиметрия (легкий уровень) Трапеция
Решение

ΔАВСД — равнобедренный.
АН = (а + в)/2 = 16.
S = ((а + в)/2)*СН.
192 = 16*СН.
СН = 12.
АС = √(16² + 12²).
АС = 20.
Ответ: 20.
Задание №19. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 8.
Найдите площадь закрашенной фигуры.

Планиметрия (легкий уровень) Площади фигур
Решение
Задание №20. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
. Какие из следующих утверждений равны?
1) Если длины сторон треугольника равны 5, 7, 9, то одна из медиан имеет длину .
2) Если две стороны и угол одного треугольника равны двум сторонам и углу другого треугольника, то такие треугольники равны.
3) Внутренние углы правильного пятиугольника равны 108° .
Планиметрия(теория)
Решение
2. Сумма углов правильного пятиугольника 180º * (5 — 2) = 540º.
Ответ: 1,3.
Задание №21. Решение варианта №226(усложненный) ОГЭ ОГЭ по математике
Решите уравнение:
(12x + 11)²(2x + 5)(3x — 2) = -11.
Рациональные выражения
Решение
Задание №22
Первую треть трассы автомобилист ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч.
Найдите скорость автомобилиста (в км/ч) на последней трети пути, если средняя скорость на всём пути равна 88 км/ч.
Текстовые задачи(средний уровень) Задачи на движение
Решение

Ответ: 110.
Задание №23
Постройте график функции:

Найдите все значения p , при каждом из которых прямая y = p имеет с графиком функции нечётное число общих точек.
Построение графиков (параметр)
Решение

Задание №24
Окружность касается стороны BC треугольника ABC в точке M , а продолжений сторон AB и AC – в точках P и Q соответственно.
Вписанная окружность треугольника ABC касается стороны BC в точке K , а стороны AB – в точке L . Отрезок AP равен 7.
Найдите периметр треугольника ABC .
Планиметрия(средний уровень) Треугольник
Решение

Ответ: 14.
Задание №25
Описанная окружность треугольника ABC пересекает стороны AD и CD параллелограмма ABCD в точках L и K . Пусть M – середина дуги KL , не содержащей точку B . Докажите, что DM перпендикулярно AC .
Задачи на доказательство (геометрия)
Решение
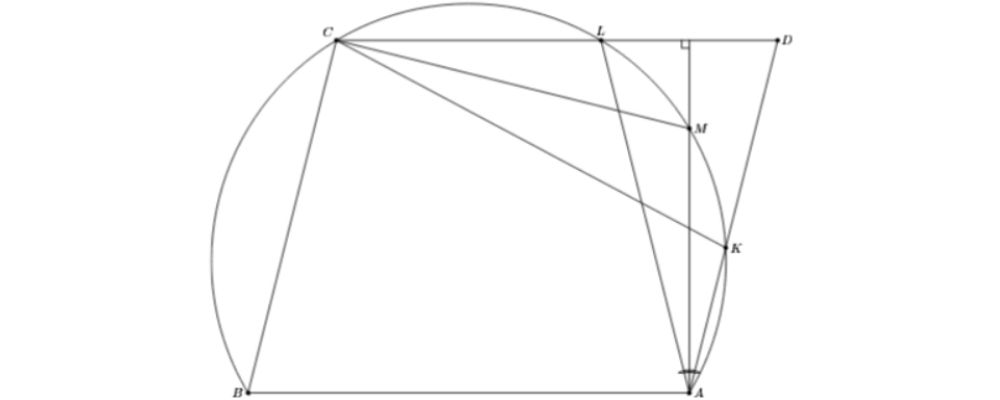
Из условия следует, что ALCB – равнобедренная трапеция, то есть AL = AD (см. рис.). При этом прямая AM – биссектриса, а значит, и высота равнобедренного треугольника ALD. Поэтому AL ⊥ СD. Аналогично CM ⊥ AD. Следовательно, M – ортоцентр треугольника ACD, и DM ⊥ AC.
Ответ: доказано DM ⊥ AC.
Задание №26
Противоположные стороны четырёхугольника, вписанного в окружность, пересекаются в точках P и Q .
Найдите PQ , если касательные к окружности, проведённые из точек P и Q , равны 28 и 45.
Планиметрия(сложный уровень)
Решение

Применим теорему о касательной и секущей.
Допустим 28 = a, и 45 = b.
Пусть DA и CB пересекаются в точке Q, BA и CD — в точке P, а окружность, описанная около треугольника ABQ, пересекает отрезок PQ в точке M.
Поскольку — BMP = BAQ = BCD = 180o — BCP, то около четырёхугольника CBMP можно описать окружность.
Тогда QM . QP = QC . QB = QA . QD = b2, PM . PQ = PA . PB = PC . PD = a2.
Сложив по членное эти равенства, получим, что
a2 + b2 = QM . QP + PM . PQ = PQ(QM + PM) = PQ2.
Следовательно PQ = √(a2 + b2) = √(282 + 452) = 53.
Ответ: 53.
